startfähige Dateien | ||
| ||||||||||||||||||||
Das dezimale ZahlensystemWir haben zehn Finger und zehn Zehen (die meisten von uns). Das fiel irgendwann mal einem Araber auf und der machte ein Zahlensystem draus. Wir mußten es als Kind erst erlernen, später ging es uns in Fleisch und Blut über. Wer denkt noch, wenn er die Zahl "235" liest, an seine Finger und Zehen?In der Volksschule (anno 1964) lernte ich, daß die Zahl 235 aus 2 Hundertern, 3 Zehnern und 5 Einern besteht. Die Kinder von heute lernen es ganz genauso. Auch die Mathematiker in den Universitäten finden, daß das stimmt. Aber, so wie Wissenschaftler halt sind, sie drücken es ein wenig anders aus: 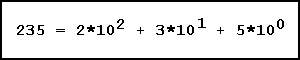 gesprochen: 235 ist gleich 2 mal 10 hoch 2 plus 3 mal 10 hoch 1 plus 5 mal 10 hoch Null. Wow! Mit den 10 zum Quadrat sind wir sofort einverstanden, jeder weiß, daß 10 hoch 2 gleich hundert ist. Daß man 10 auch als 10 hoch eins schreiben kann, ist vielen älteren Leuten nicht klar, erscheint aber nach kurzem Nachdenken logisch. Schwer wird es bei den fünf mal zehn hoch Null. Ein mathematisches Axiom sagt: Jede Zahl (ungleich Null) hoch Null ist gleich Eins. Also ist die Aussage "...plus 5 mal 10 hoch Null" nur eine andere Umschreibung für "...und fünf Einer". Irgendeine Zahl hoch Null zu nehmen, ist ein beliebter Trick bei Mathematikern, wenn sie grade mal schnell eine Eins brauchen. Wenn wir oben im Bild die Hochzahlen betrachten, stellen wir fest, daß sie von rechts beginnend nach links hochlaufen. Die Reihenfolge ist Null, Eins, Zwei. Wäre die Zahl größer, z.B. 7235, dann wäre vorne zu sehen: "Sieben mal 10 hoch 3". Denn wir wissen, daß 10 hoch 3 genau Tausend ergibt. Die nächste Zahl in der Reihenfolge der Hochzahlen wäre also für die Tausenderstelle die Drei. So laufen die Hochzahlen für jede Stelle einer beliebigen Zahl von rechts nach links immer um eins weiter hoch. Wenn wir für 25 Euro Lotto spielen, dann geben wir
2 mal 10 hoch 1 plus 5 mal 10 hoch 0 Euro aus. | ||||||||||||
Das binäre ZahlensystemComputer haben keine Zehen. Sie haben Bits. Diese Bits können sie an- oder abschalten. Die Bits haben Strom oder sie haben keinen Strom. Mathematisch sagt man:Das Bit ist entweder Null oder es ist Eins. Wenn man ein paar Bits aus dem Arbeitsspeicher nebeneinanderlegt, entsteht ein Bitmuster. Bits werden in Gruppen zu jeweils 8 Bit zusammengefaßt. Eine solche Bitgruppe nennt man "Byte". Dieser Begriff ist aus der Computersteinzeit. Er bedeutet: So viele Bits, wie der Computer durch einen "Biß" in den Arbeitsspeicher "abbeißen" kann. Also acht Stück. Das ist natürlich mittlerweile von der Technik längst überholt, aber der Begriff ist geblieben. Die Handhabung des binären oder auch dualen Zahlensystems geschieht analog zum dezimalen System. Beim dezimalen System ist aber die Basis gleich 10 und wir haben die Ziffern 0 bis 9, beim binären ist es die 2 und wir haben die Ziffern 0 und 1. Die Umrechnung des Wertes einer Binärzahl geschieht genauso, wie der Wert einer dezimalen Zahl ermittelt wird (siehe oben). Statt Einer, Zehner, Hunderter usw. sind es hier Einer, Zweier, Vierer, Achter ... etc. Am besten betrachten wir ein Beispiel:  Das Lesen von Binärzahlen stellt also kein großes Problem dar. Haben Sie alles begriffen? Hier sind Aufgaben zum Thema:  | ||||||||||||
Das hexadezimale ZahlensystemVoraussetzung für das Verständnis dieses Abschnittes sind das dezimale Zahlensystem und das binäre Zahlensystem.Das hexadezimale Zahlensystem funktioniert analog zu den bereits vorgestellten Zahlensystemen. Eigentlich funktioniert absolut jedes Zahlensystem nach diesem Muster. Im binären System gibt es Einer, Zweier, Vierer, Achter, Sechzehner usw. Im dezimalen System gibt es Einer, Zehner, Hunderter, Tausender usw. Im hexadezimalen Systm gibt es Einer, Sechzehner, Zweihundertsechsundfünziger usw. Im binären System brauchen wir weniger als 10 Ziffern: Nur noch zwei. Im hexadezimalen System brauchen wir mehr als 10 Ziffern: nämlich 16 Die ersten 10 Ziffern ( 0 bis 9 ) entsprechen den bereits bekannten Ziffern. Für die Werte 10 bis 15 werden die Buchstaben A bis F gesetzt. So entspricht also der hexadezimale Wert D dem dezimalen Wert 13. Wieviel ist ein AFFE?
Haben Sie alles begriffen? Hier sind Aufgaben zum Thema:  | ||||||||||||
| Letztes Update am 5.12.08 Alles neu | 
 |
|
| |